Strong/Strong Titration Graph

Let's look at how the pH changes during a strong/strong titration from a graphical perspective. (A weak titration graph is found here) 

We will be looking at this for the problem here:

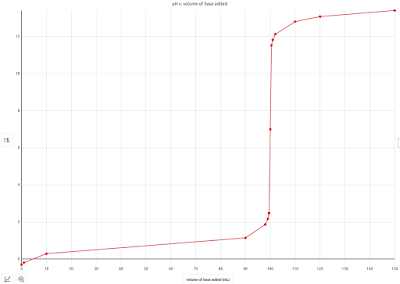
50.00 mL of 2.00 M HA (an imaginary acid) are titrated with 1.00M XOH (an imaginary base). What will the pH be before any base is added and after additions of 1.00 mL, 10.00 mL, 50.00 mL, 98.00 mL, 100.00 mL, and 120.00 mL of the base?

We did all of the calculations here, so if you haven't looked through those yet, it would be worth checking out.

If we graph the points from that problem, we get this:

Adding in a few more points to "smooth" things out a bit, we get this:

In simplest terms, at the beginning, when we have excess acid, the solution is acidic (with a low pH). When we to equivalence, the pH becomes 7. Once we pass the equivalence point, the solution contains excess base and the pH is high.

The equivalence point is the middle of the steep vertical part of the graph. Stated differently, the equivalence point is the point in the graph where the slope is the most vertical.

We can find that point graphically, by making a graph of the slope vs. volume of base added. For those of you with some level of higher math, this is simply the derivative of the previous graph.

If it helps to visualize what this graph is showing, here are the two graphs on the same axes: