Let's consider multiple temperature and phase changes

Here's a more complex problem:

How much heat is required to change 10.0 g of ice at -14^oC into steam at 151^oC?

Since we now know that there are different formulas for heat associated with temperature changes and heat associated with phase changes, we need to look carefully at what will happen as heat is applied.

When the ice is heated, what happens first?

It is tempting to answer that it will melt, but that’s not right.

The ice isn’t warm enough to melt. It must first warm up to 0^oC. After that, it can melt. During the process of melting, the temperature will not change resulting in 10.0 g of liquid water at 0^oC. If we continue to heat it, the water will warm up to the boiling point (100^oC). The water will then boil (with no change in temperature). Additional heat will then be needed to warm the steam up to 151^oC.

In simpler terms, this is a 5 step process:

1. ice warming from -14^oC to ice at 0^oC 
2. melting ice
3. water warming from 0^oC to 100^oC
4. boiling water
5. steam warming from 100^oC to 151^oC 

Or, if you prefer pictures…

Each step requires heat and each step must be calculated separately. The heat required for the entire process will then be the heat of the five steps added together.


Each step requires heat and each step must be calculated separately. The heat required for the entire process will then be the heat of the five steps added together.

Calculating the heat of each step is straightforward.If the process involves a temperature change, the formula is

If it involves melting (or freezing if we're cooling things down), the formula is

And if it involves boiling (or condensing if we're cooling), the formula is

So, visually, the calculation looks like this:

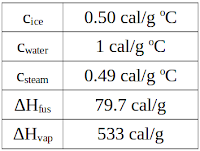
Be careful! The specific heat of steam, water and ice are all different and the heat of fusion and heat of vaporization are also different.

Here are the values we will need to finish this problem:

The math for each step can be seen here:

And the total amount of heat is calculated by adding the heats of the 5 steps like this

Note: If we wanted to calculate the heat that needed to be removed in order to reverse this process, we would do exactly the same math with one VERY important distinction. ALL of the ΔT values would be negative and both the ΔH_fus and the ΔH_vap would need to be entered as negative values, since we remove heat to condense and freeze a substance.

Another way to think about the process can be found here.