Strong and Weak Acids and Bases

There are, as I’m sure you have realized by now, a number of words that chemists use differently from “normal people.” One of those words is “strong” as it relates to acids and bases. When a “normal person” talks about a strong acid, they mean that the solution is dangerous. When a chemist uses the term, they mean that the Ka value for the acid is large.

Chemists know that what makes an acidic solution dangerous is the concentration of the hydronium ion in the solution. That is why pH is such a useful measurement - it is a value based directly on the [H3O+1].

As explained here, the amount of hydronium present in a solution depends on BOTH the initial concentration of the acid and the value of Ka. So, two acids can have the same initial concentration, but very different pH values if they have very different Ka values. At the same time, it would be possible to have two acids with very different Ka values but the same pH if the starting concentration of the solutions were very different. 

Let’s see how this plays out in the real world. We’ll look at two acids, hypochlorous acid (HClO) and hydrochloric acid (HCl). Hypochlorous acid is considered a weak acid (with a Ka=2.9x10-8), hydrochloric acid is a strong acid (with Ka ~ 106).

Let’s find the pH of a 0.100 M solution of each acid.

For hypochlorous acid (our WEAK acid) the ICE table will look like this

The equilibrium expression will be:

This will be a “little x” problem. Solving gives us x = 5.39x10-5, so [H3O+1] = 5.39x10-5 M and the pH = 4.27.

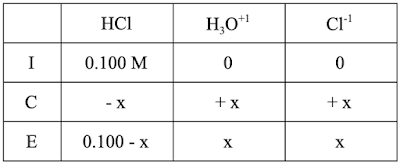
Now, let’s try the same problem for HCl (our STRONG acid). The Ice table will look essentially the same:

and the equilibrium expression will also look essentially the same:

There are, however, two important and related differences

1. We don’t have an actual value for Ka.

2. Ka is large, which means that this is a “big X” problem. 

For a big X problem we will run the reaction entirely (until we have a concentration of 0). We can determine when that happens by setting the “subtraction problem” = 0. 

[0.100 - x] = 0

That will give us x=0.100. Substituting that into the bottom row of the ICE table will create a NEW problem with this new ICE table:

This will give us this equilibrium expression

This time we have a “small y” problem, but we still don’t have the actual value of Ka so we cannot solve this problem for y.

This is not actually a problem, however. Remember that we are looking for pH. That only requires us to know the [H3O+1], not ALL of the concentrations. In other words we don’t need to know what “y” is. We only need to know that it is small enough so that (0.100 - y) ≈ 0.100. This is true, so [H3O+1] = 0.100 M and pH = 1.00

In the problem with the large Ka value (a STRONG acid), the final [H3O+1] = the initial [acid]. This ALWAYS works for strong acids, that is acids with large Ka values!

What All of This Means

1. When Ka is big enough, you don’t have to do any math to get [H3O+1]. You automatically know that it will be the given initial concentration of the acid. These are called strong acids.

2. The same rule can be applied to bases with large Kb values, except that in those cases the [OH-1] = initial [base]. These are called strong bases.

The Strong Acids and Bases

There are LOTS of weak acids and weak bases, but the list of common strong acids and common strong bases are both pretty short - short enough that you should memorize them.