Bohr went further. He found the meaning in the equations or Balmer, Paschen and Lyman. Remember that the three equations looked like this:
If we rearrange those equations so that they are “in order” in terms of the energy the light carries (UV, then visible, then IR) we get this:
What Bohr saw was that the 1 in the Lyman equation could be thought of as 11, which would mean that all three equations had the exact same format.
He further noted that the bottom of the first fraction was, in each case, a perfect square. Thus, the three equations could actually be written as one single equation with two variables.
With this equation, Bohr had a mathematical basis for his theory. “N” was the ring, or energy level, the electron was dropping from and “a” was the ring it was landing on.
Thus UV light was released by a Hydrogen atom when an electron dropped down to level 1 from a higher orbit. Visible light was produced if the electron dropped to level 2 and IR light when it dropped only to level 3.
Lastly, since Bohr was concerned about the quantization of energy, he transformed the equation. We know that energy depends on the frequency of a wave (in this case a light wave) and that frequency is inversely related to wavelength. Specifically, we know these two equations:
where E is energy, h is Planck’s constant, ν is frequency, c is the speed of light and λ is wavelength. By combining and rearranging these equations, we can see that:
that allowed Bohr to solve the equation from Balmer, Paschen and Lyman for energy, giving him:
where k is RH⋅h⋅c, and the negative sign indicates that the energy is emitted (rather than absorbed) when an electron drops.
Of course, even after all of this success, the theory still has problems.


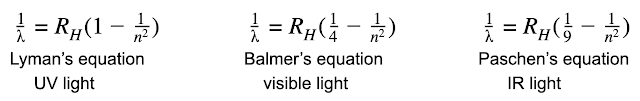





No comments:
Post a Comment