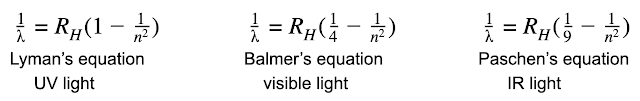Schrodinger's Waves and the Multi-Electron Atom

If an electron in an atom can be thought of as a single violinist, then an atom with multiple electrons is string quartet, or octet, or a full orchestra. Setting aside the difficulty of suspending an entire orchestra in mid-air, imagine what the sound would now look like.

The sound would still be a sphere but with a few changes:

• The sphere would certainly be bigger. Even if all of the players are playing quietly, the sound of the orchestra will be louder (and bigger) than that of a single player.
• The sound would not be a single shade of green anymore. Instead, I imagine a constantly changing rainbow of sound - pulsing and throbbing. 

Symphony No. 1
by Brahms

Great musicians and musical scholars can listen to an orchestral piece and pick out the individual lines and notes played by the different instruments, but most of us just hear “the orchestra”. 

In the same way, great physicists might be able to see (or calculate) the sound of JUST the strings, or JUST the oboe, and they might see interesting shapes and twists within the larger bubble of sound. 

What makes great music (orchestral, country, R&B, whatever) is the interplay of the sounds, sometimes reinforcing each other, sometimes “arguing” with each other, but in all cases combining to make one overarching sound. 

 Electrons in atoms play the same way. The waves (the electrons) sometime reinforce each other, sometimes “argue”, but in the end they create an electron structure of the atom that defines the properties of that atom.

The image on the left is the atomic equivalent of an orchestral score, showing many (not even all) of the different wave forms that an electron can take in an atom separated out. This is how great musical scholars can "hear" an orchestra, and in this case, how physicists and chemists think about individual electrons in an atom.

The image on the right is an image of a molecule made of several atoms as it breaks apart. Each "blob" in that picture is an atom with all of its "musicians" playing together. What we see is the big picture - the sound of the orchestra.

Let's take a (very basic) look at the math that generated these images.

Kc and Kp

Equilibrium systems often include gases, and systems that are entirely composed of gases are fairly common. It is therefore important to take a closer look at these systems. Specifically, we’ll take a look at the properties of gases that we most commonly work with and how these measurements relate to equilibrium.

Let’s start with the Ideal Gas Law (PV=nRT). We can rearrange this formula like this:

You don’t need to know why I chose to rearrange that way yet. You’ll see soon enough. Of course we know that moles over liters is molarity, so that equation can be rewritten as:

or, using the notation we use when we do equilibrium problems, we could get:

Now, let’s put that to work in an equilibrium setting. We’ll use this reaction for our purposes:

2 SO2 (g) + O2 (g) ⇄ 2 SO3 (g) 

The equilibrium expression for this reaction is:

We can now substitute the formula above, which will give us:

This is beginning to look a little horrible, but bear with me. We can factor out the RT values (remembering that dividing by a fraction is the same as multiplying by the reciprocal). That will give us this:

We can combine like terms to get

then simplifying, gives us

Obviously, the exponent on the right is 1, but we'll leave it like this to make the point that we've been heading for on this page

On the left of the equation we have K. This is the equilibrium constant we've been using all along. It is sometimes written as Keq. In this context, we're going to label it Kc, since it is the equilibrium constant written in terms of concentration.

In the first set of parentheses we have something that has EXACTLY the same form as K except that it is written in terms of pressure values, rather than concentration. We'll call that KP. The last factor in the equation is RT (the gas constant x the temperature) raised to 3-2, which happens to be the moles of reactants - moles of products.

All of that is a long-winded way of saying that we can write this equation

It is also commonly written this way (although both are mathematically equivalent)

Why do we care?

In the end, after all of this algebra, there are a few simple and important ideas:

1. The equilibrium expression can be written as Kc (using concentrations) or as KP (using pressures)

2. Kc and KP are related but not equal (unless the moles of products = moles of reactants)

3. Equilibrium problems involving gases can be solved using EITHER concentrations (with Kc) or pressures (with KP).

Electron configuration - Negative Ions

Now that you have a sense of electron configurations and how electrons are arranged in the orbitals of an atom, it is time to look at ions, specifically negative ions.

Remember that a set of orbitals with the same energy is most stable when it is empty, half-filled or filled. To understand negative ions, we will focus on the last of those three possibilities - when the orbitals are filled and in particular how it applies to the p block of the periodic table.

The p block can hold up to 6 electrons (3 orbitals, 2 electrons in each). The result of that is a column of remarkably stable elements - the noble gases.

Elements that are close to those elements often take electrons from other atoms to achieve that same stable electron configuration. For instance fluorine has an electron configuration of 1s2 2s2 2p5, which is almost the same as neon (1s2 2s2 2p6). If fluorine steals an electron from another atom, it achieves the same, stable structure that neon has. As a result the F-1 ion is very stable. 

This can be confusing, so let’s make sure that what we’re saying here is clear.

• Fluorine is unstable and dangerous (1s2 2s2 2p5)

• Fluorine often steals an electron from another atom to become stable (1s2 2s2 2p6)

• The F-1ion (called fluoride) is so stable and safe that we rub it on our teeth.

The same is true of other elements. For instance, chlorine is a dangerous corrosive gas. In fact, it was the first gas used as a chemical warfare agent by the German’s in WWI. Chloride (the Cl-1 ion) created when chlorine steals an electron from another atom is so safe we put it in almost everything we cook (It’s half of table salt).

Other elements will steal more electrons as needed to achieve a "noble gas structure." For instance, the most common charge that oxygen (normally 1s2 2s2 2p4 ) has in nature is -2 because the O-2 ion has an electron configuration of 1s2 2s2 2p6.

Amphoteric Compounds and Ions

There are a number of compounds and ions that can act as either acids or bases. The term for such things is amphoteric. (The “am” prefix means “either” and is used in words like ambidextrous - someone who can use either hand to write and do other things, and amphibian - animals that spend some time on land and some in the water.)

Amphoteric Compounds

In order to be an acid, a compound must have an H to give away. Generally, in chemistry classes, any H’s are at the beginning of the formula. In order to be a base, a compound must have a lone pair of electrons that can bond with an H+1 ion (Lewis’s definition). So, compounds that start with an H and have an O or N atom (with lone pairs) are the most common examples in chemistry classes. In biology classes, the formulas are a little more cryptic, but generally they are compounds that have a COOH group (that’s a carbon double bonded to ONE oxygen and single bonded to an O-H) and also an amine group (that’s an N atom with 2 H’s and a lone pair). These are called amino acids and an example is shown here:

Amphoteric Ions

It is easy to spot amphoteric ions in chemistry class. These are ions that start with an H (which can be given away) and end with a negative charge (that can attract to an H+1 ion). Basically, the list is all of the “bi” ions, like bisulfate (HSO4-1) or biphosphate (HPO4-2).

How will an amphoteric compound or ion behave?

Whether an amphoteric compound or ion will act as an acid or a base is determined primarily by what it is with. Anything that is amphoteric will react as an acid if it is placed with a strong base and will act as a base if mixed with a strong acid. When mixed with a weak acid or base, only a mathematical comparison of the relevant Ka and Kb values will tell.

Problems with Bohr's Atom

Bohr’s theory does an excellent job of explaining the production of light and the Hydrogen spectrum. Of course, nothing is ever easy.

There are only two problems:

a) the math, and

b) the theory

In other words, everything.

Let's look at those two things separately.

The problem with the theory:

Electrons, according to Bohr, jump instantaneously from one ring to another. Understand that Bohr has not claimed that the electrons move from ring to ring. That would require them to be in between levels (an impossible amount of potential energy). Bohr's theory requires electrons to move instantaneously from one ring to another without ever being in between them. This is, of course, physically impossible.

The problem with the math:

Bohr's math predicts the energy and wavelength of the light emitted by a hydrogen atom perfectly. However, the math doesn't work for anything with more than one electron. In other words, it works for Hydrogen, and for a He+1 ion, etc. but doesn't work for an atom of helium.

Since the theory explains the production of light and the math works for hydrogen, we know that there must be some truth to it. However, since the math doesn’t work for MOST things, there must be some real flaws.

It is sometimes easy for students to wonder why we talk about Bohr at all. After all, if he’s wrong, the thought goes, let’s just get to what’s right. So, it’s important to understand that MOST of what Bohr has said IS right.

To be specific:

1. Energy IS quantized.

2. Electrons DO occupy energy levels in atoms

3. Electrons DO generally occupy the lowest energy level they can

4. When energy is added to an atom, electrons DO move to a higher level

5. That energy is emitted (as light) when the electron drops back down

 

So, what’s wrong? 

The energy of electrons is not JUST potential energy. 

That may seem like a little flaw, but remember it was that idea that created Bohr's picture of rings (or orbits) around the nucleus. If we take away the constraint of potential energy, the picture itself dissolves. 

So, the common image of the atom, seen here, is wrong.

So, what do we replace it with? For that we need to go deeper into quantum theory, starting with the photoelectric effect.

Werner Heisenberg's Uncertainty Principle

In 1927, Werner Heisneberg published the Uncertainty Principle. As a mathematical formula, is looks like this:

Δx⋅Δp≥(h/4π)

In simplest terms, the principle states

that the "uncertainty in the measurement of position times the uncertainty in the measurement of momentum is always greater than or equal to a very small number."

Okay, that wasn’t simple. So, let’s pull apart the ideas

Uncertainty in measurement

Any time you make a measurement there is some inherent uncertainty. Let’s imagine that you want to measure the length of a pencil mark on your paper. You lay down a ruler and measure the mark to be 4.3 cm. If you picked up the ruler and measured it again, assuming that you were careful, you would get the same value. But, if I then handed you a ruler marked to the hundredth of cm (and a magnifying glass) you might get 4.28 cm or 4.31 cm. If you picked the ruler up and laid it back down, you would be less likely to get exactly the same measurement. If I found a ruler that measured to the thousandths of a cm, you would have an even harder time consistently getting exactly the same value. The line isn’t changing. This is just proof that your measurement is not perfect. The imperfection (the changeable amount) in your measurement is the uncertainty.

Recognizing that, your second measurement might be recorded as 4.30 +/- 0.02 cm.

Multiplying uncertainties

Heisenberg’s Principle looks at the product of two uncertainties (position and momentum). When a product of two values is equal to a constant, they have an indirect relationship (as one goes up, the other goes down. (In other words, if x⋅y =10, as y gets smaller, x has to get bigger for the math to still work.) 

In this case, as the uncertainty of the position goes down, the uncertainty of the momentum goes up. In English - the more precisely we know the momentum of something, the less precisely we can know it’s location. 

A very small number

The very small number mentioned above is approximately 5.3x10-35 (which is Planck’s constant divided by 4π). This means that the Uncertainty Principle doesn’t matter for large things like planets, or people, or ants or even bacteria and viruses. It does matter however for electrons.

Why we (chemists) care

Because Heisenberg says (correctly) that we can’t know exactly where an electron is and how it is moving, it becomes logical, and even required to discuss and calculate the probability of an electron’s location and behavior, rather than trying to be specific.

Historical Figures are Never Easy

Werner Heisenberg is a complicated figure. Early in his career he studied with Neils Bohr in Copenhagen and the cooperative work they did led to some of Bohr's best work and to Heisenberg’s most famous work, the Uncertainty Principle. However, Heisenberg was a German, and ended up leading the Nazi attempt to develop a nuclear bomb.  After the war, Heisenberg was captured, held and questioned by the British. During that time, he claimed that he had sabotaged the Nazi bomb effort from within, to ensure that Hitler never gained access to such a weapon. Others have said that there is no evidence of his subterfuge and that he simply was unable to accomplish the task. At this point, the truth may never be known.

Bohr's Math

Bohr went further. He found the meaning in the equations or Balmer, Paschen and Lyman. Remember that the three equations looked like this:

If we rearrange those equations so that they are “in order” in terms of the energy the light carries (UV, then visible, then IR) we get this:

What Bohr saw was that the 1 in the Lyman equation could be thought of as 11, which would mean that all three equations had the exact same format. 

He further noted that the bottom of the first fraction was, in each case, a perfect square. Thus, the three equations could actually be written as one single equation with two variables.

With this equation, Bohr had a mathematical basis for his theory. “N” was the ring, or energy level, the electron was dropping from and “a” was the ring it was landing on.

Thus UV light was released by a Hydrogen atom when an electron dropped down to level 1 from a higher orbit. Visible light was produced if the electron dropped to level 2 and IR light when it dropped only to level 3.

Lastly, since Bohr was concerned about the quantization of energy, he transformed the equation. We know that energy depends on the frequency of a wave (in this case a light wave) and that frequency is inversely related to wavelength. Specifically, we know these two equations:

where E is energy, h is Planck’s constant, ν is frequency, c is the speed of light and λ is wavelength. By combining and rearranging these equations, we can see that:

that allowed Bohr to solve the equation from Balmer, Paschen and Lyman for energy, giving him:

where k is RH⋅h⋅c, and the negative sign indicates that the energy is emitted (rather than absorbed) when an electron drops.

Of course, even after all of this success, the theory still has problems.