Setting up an ICE Table

ICE tables are the first step to solving Equilibrium problems. Even working chemists use the ideas behind ICE tables to solve equilibrium problems. So, let's start at the beginning.

ICE stands for:

I - Initial concentrations

C - Change that occurs during the shift to equilibrium

E - Equilibrium concentrations

Let’s look at a specific example to see how this works:

The reaction A + 2 B ⇄ C + 3D has a Keq = 4.63x10-12. If 1.00 mole of A and 2.00 moles of B are placed into an evacuated 2.00 L container, what will the concentrations be when equilibrium is reached?

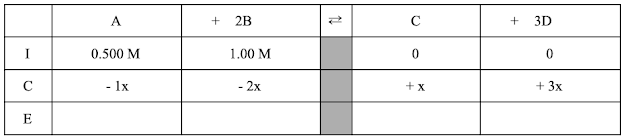
We’ll start setting up the ICE table like this:

Next we’ll enter what we know (the information on the “I” line), remembering that M is moles/L.

Next, we need to know which direction the reaction is running. In this case, it must be running to the right since there are currently no product molecules.

Since the reaction is running to the right, we know that the concentrations of A and B will be decreasing, while the concentrations of C and D will be increasing

We don’t know how much the reaction will run forward, so we don’t know how much the concentration of C will increase. From our math class experiences, we know that if we don’t know something, we can put in a variable. Let’s use “x”

Now, we can use our stoichiometry logic to figure out the rest of the “C” row. Every time the reaction runs forward, it makes 3 times as many “D” molecules as “C” molecules. So the change in D will be + 3x. At the same time, the reaction used 1 “A” and 2 “B” molecules, so those changes will be - 1x and -2x respectively. Here’s what the ICE table looks like now:

Now we can fill out the “E” row by combining the rows above. For example, the equilibrium concentration of B will be 1.00 M (what it started with) - 2x (whatever “x” is). Here’s our final, finished ICE table:

Once our table is set up, we can then substitute in our values on the “E” row for the concentrations in the equilibrium expression, like this:

Suddenly, it's just an algebra problem with one variable. Of course, we still need to solve it, but that's another page.

A Note about Coefficients

At some point when learning how to solve equilibrium problems, many students are suddenly struck by the fact that the coefficients in the reaction have been used twice (once for the exponents in the equilibrium expression, and once for the "number of x's" in the concentrations. This is CORRECT. The number SHOULD be used twice.